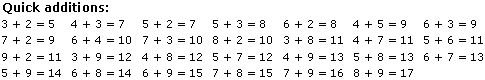Number System - Problem Set 1
Saturday, April 29, 2006
Test your knowledge
Problems are based on the basics which we have covered in number system. Try to solve the questions first and then look at the answers. If you have any doubts refer to Basics 1 and Basics 2 of Number System.
Questions:
Q1) 8 odd natural numbers add up to a total of 77. Which one is true?
a) One of the number has to be 1.
b) One of the number has to be 3.
c) One of the number has to be 7.
d) One of the number has to be 5.
e) There is no solution for this.
Q2) P is product of three consecutive natural numbers, Which one is true?
a) P will always be divisible by 24.
b) P will always be divisible by 10.
c) P will always be divisible by 6.
d) No solution.
Q3) 45556 x 23843 = ?
a) 1086194751
b) 1087161425
c) 1086194723
d) 1086191708
Q4) 123 + 345 + 524 + 245 = ?
a) 1137
b) 1224
c) 1076
d) 1138
Q5) 47^4 = ?
a) 4873634
b) 4879681
c) 4878646
d) 4870682
Q6) Which of the numbers are prime?
a) 67
b) 113
c) 317
d) 144
Solutions:
A1): e, Do you remember, sum of any odd numbers of even number (i.e 8) is even. We have seen this in basics.
A2): c, We have seen that product of 3 consecutive numbers is always divisible by 6, If it would have been mentioned that the first number of the three numbers is even, then the product would be always divisible by 24..
A3): d, Why? The units digits of the numbers are even and odd, so even x odd = even, only one option satisfies this, hence by elimination. Or, You could just multiply the last digits of the two numbers and looked for the last digit of the options.
A4): a, Three numbers are even and one is odd so, odd + even + even + even = odd. Only one option is odd, hence by elimination. Or, just add up all the last digits of the numbers and look for the last digit in the options. Quick maths will help you here.
A5): b, Anything raised to an odd number (here base is odd), the result is odd, hence by elimination. There is a concept of cyclicity, which I will cover later.
A6): a, b and c are primes. Try it with the square root method that we have seen earlier, I will explain for 67,
Step 1) The square root of 67 will lie in between of 8 and 9, we take the greater number i.e 9,
Step 2) Try to divide 67 with all the primes less than 9, i.e 2, 3, 5, 7. None of the numbers divide 67, hence 67 is a prime number.
*There will be more Problem Sets on Number System in which I will cover past CAT questions and other CAT/GMAT like questions.
Arithmetic - Basics 3
Friday, April 28, 2006
Suppose you want to find if the number 9475724 is divisible by 4, what will you do? Will you divide the whole number and check if it is divisible or not? If yes, then wait, there are aesthetic methods to do so.
Divisibility tests:
2: If the units place of the number is even, the number is divisible by 2, e.g. 2, 4, 6, 8 and 0.
3: If the sum total of digits of the number is divisible by 3 then the number is divisible by three, e.g. 633 = 6 + 3 + 3 = 12, which is divisible by 3, hence the number 633 is also divisible by 3.
4: If the last 2 digits of the number is divisible by 4, the number will be divisible by 4.
5: If the units place of the number is divisible by 5, means should be 0 or 5, the number will be divisible by 5.
6: If the units place of the number is divisible by 2 and 3 both then the number is divisible by 6.
7: For 7 the method is little different, let us look at an example, suppose you want to find if 6764 is divisible by 7 or not. We have to start from left to right, i.e from units place, take 4 multiply it with 2 and subtract it with remaining i.e 676, then whatever the answer take its unit place multiply with 2 and subtract with remaining, go on doing until you are left with a number that you can easily identify as a multiple of 7 or not.
Step 1) 676 - 4 x 2 = 676 - 8 = 668
Step 2) 66 - 8 x 2 = 66 - 16 = 50, stop here, you know 50 is not a multiple of 7, so we can peacefully say that the number 6764 is not divisible by 7. Later we will see why we took 2 as a multiple.
8: If the last 3 digits of the number is divisible by 8, the number is also divisible by 8, also if the last 3 digits are 0's. Actually there is a easier method, see if the last 2 digits are divisible by 4 and the hundred's place digit is odd, then the number is divisible by 8 or if the last 2 digits are divisible by 8 and the hundred's place digit is even, then the number will be divisible by 8.
9: If the sum total of digits of the number is divisible by 9 then the number is divisible by nine, similar to divisibility rule for 3.
11: If the sum difference of even numbers and odd numbers is divisible by 11 or is 0, then the number is divisible by 11, example take 13574.
Step 1) 1 + 5 + 4 = 10, All the digits in the odd places.
Step 2) 3 + 7 = 10, all the digits in the even places
Step 3) 10 - 10 = 0, their difference, hence the number is divisible by 11.
12: If the number is divisible by 4 and 3 then the number is divisible by 12. Wonder why we check for 4 and 3? Because the factors of 12 are 4 and 3 and they are co-primes.
Some Observations:
1) If z divides both x and y, then (x + y) and (x - y) are divisible by z.
Example: 2 divides both 4 and 12, so (4 + 12) and (4 - 12) will both be divisible by 2.
2) Sum of 5 consecutive whole numbers is always divisible by 5.
Example: 1 + 2 + 3 + 4 + 5 = 15, hence divisible by 5.
3) The product of three consecutive numbers, if the first number is even, the result will always be divisible by 24. Why? Because the above numbers will always have factors 8 and 3.
Example: 2 x 3 x 4 = 24 or 4 x 5 x 6 = 120, both the numbers, 24 and 120 are divisible by 24.
4) The product of three consecutive numbers, if the first number is odd, then the result will always be divisible by 6. Why? Because the above numbers will always have factors 2 and 3.
Example: 3 x 4 x 5 = 60 or 5 x 6 x 7 = 210, both the numbers, 60 and 210 is divisible by 6.
5) Difference between a number and the number formed by writing its digits in reverse order is divisible by 9.
Example: 4321 - 1234 = 3087, which is divisible by 9. (Remember, if the sum of the digits is divisible by 9, then the number is divisible by 9.)
6) Any number (10^n) - 1 is divisible by 9.
Example: 10^3 - 1 = 1000 - 1 = 999
Permalink / 3 comments /
Arithmetic - Basics 2
Thursday, April 27, 2006
Previously we worked on how to easily add large numbers, but what if numbers are to be subtracted? Same method won't work. We have to make minor modifications in our method for that. Actually its quite simple, lets sharpen our pencils and get ready for fun.
Say you want to add and subtract few numbers at same time, suppose 8565 - 329 + 952. We start from units place, same as in Addition method.
5 - 9 + 2 = - 2
Because the result is in negative we Borrow 1 from 10's place of a positive value. Suppose we borrow from 8565, we can even borrow from 452, because its positive too.
We can subtract the answer from 10, because we have borrowed 1 from a positive value (i.e 10 - 2 = 8).
....-1
8565 - 329 + 952 = ---8
Next we continue with the 10's place i.e 6(-1) - 2 + 5 = 8
....-1
8565 - 329 + 952 = --88
Next we continue with the 100's place i.e 5 - 3 + 9 = 11, so we write down the units place and carry over the rest of the digits on the left side of positive number and not on the negative number means we can carry the number on 8565 and 952 but not over 329. Remember how we used to add numbers by addition method? We never count higher than 10 in our running total, you can do the same here but then you have to remember how many times you have reached the limit of 10, and carry that count.
1..-1
8565 - 329 + 952 = -188
Next we continue with the 1000's place i.e 8 + 1 = 9, so the final answer will be
1..-1
8565 - 329 + 952 = 9188
So now you are equipped with all the necessary tools that will be required to do your basic calculations.
Auf wiedersehen.
Permalink / 0 comments /
Arithmetic - Basics 1
Q) Why do we need to look into Arithmetic?
A) Of course we don't need to look into addition, subtraction, multiplication and division, if you are good with it. But theres nothing wrong in learning few tricks, we don't need to learn Vedic Maths, just few tricks to calculate faster. After all, its all about speed and accuracy, honey.
Take off!
First of all, one needs to be quick in adding numbers; this can be easily achieved if you are quick with adding one digit numbers. Every one knows 4 + 3 = 7, but it has to be in your visual memory. Can u tell the answer without calculating in your mind? If yes, then skip this section.
Bug your friends, brothers, relatives and your mom to quiz you, to ask you to add numbers. Following is the cheat sheet. Fit this in your visual memory.
When adding two numbers, one trick is to split any one of the number such that the other number can be composed as 10 when added with one part and then add the remaining part.
Example, take 8 + 6, you can spit 6 in two part 2 and 4, now add 8 with 2 which gives 10 and then add 4 to it, i.e. 14.
The easiest method to add large numbers is to start with higher order digits.
Suppose you want to add 8,500 + 2,000 + 900 + 85 + 9
1) 8,000 + 2,000 = 10,000 --- thousands places
2) 500 + 900 = 1,400 --- hundreds places
3) 10,000 + 1400 = 11,400 --- add the above two
4) 11,400 + 80 = 11,480 --- add with 10's place
5) 5 + 9 = 14 --- add the unit places
6) 11,480 + 14 = 11,494. --- the final answer
It is lot easier when done mentally, this method is meant to be done mentally ;)
There are easier ways to add numbers other than which we learned in school. In the next 5 minutes you will learn one of such method.
I will start adding all the unit places first then tens then hundreds so on and so forth. In the conventional method we add all the numbers and write down the unit's place of the sum and carry over the rest. In this method we will add the digits, but "we never count higher than 10". That means, whenever the running total becomes greater than 10, we replace the 10 with zero and go ahead, we need to keep track how many times we reduced the sum with 10, means, we need to count how many times we reduced the sum with 10 and carry that number to the left.
Suppose you want to add 14686, 15463 and 65367
Sum of all units' digits is
6 + 3 = 9
9 + 7 (sum exceeds 10 (i.e 16) so subtract 10 (i.e 16 - 10 = 6), remainder 6)
Now write down 6 and carry over 1, because the sum exceeded 10 just once.
14686 + 15463 + 65367 = ----6
Now add the tens places, don't forget to include the carry forward
Sum of all tens digits is
8 + 6 (sum exceeds 10 (i.e 14) so subtract 10 (14-10), remainder 4)
4 + 6 (sum is equal to 10 so subtract 10)
0 + 1(carry) = 1
Now write down 1 and carry over 2, because the sum exceeded 10 only twice.
14686 + 15463 + 65367 = ---16
Now add the hundreds places, don't forget to include the carry forward. Sum of all hundreds place digits is
6 + 4 (sum is equal to 10 so subtract 10)
0 + 3 + 2(carry) = 5
Now carry over the 1 and write down 5
14686 + 15463 + 65367 = --516
Now add the thousands places, don't forget to include the carry forward
Sum of all thousands place digits is
4 + 5
9 + 5 (sum > 10 subtract 10, remainder 4)
4 + 1(carry) = 5
Now carry over the 1 and write down 5
14686 + 15463 + 65367 = -5516
Now add the ten thousand places, don't forget to include the carry forward. Sum of all ten thousands place digits is 1 + 1 + 6 + 1(carry) = 9
And your final answer
14686 + 15463 + 65367 = 95516
I hope you understood the concept; we just need not exceed the running total more than 10. All this happens quickly if your are good with numbers. This might be tedious at first, but after solving few numbers you will find it lot easier than the conventional method. If you are not feeling comfortable, might be memorizing addition of one digit numbers will help. Like 7 + 8 = 7 + (3 + 5) = 15. In this example I am splitting the number 8 in 3 and 5 to make the addition easier, I know that 7 + 3 will lead me to 10. You can also split the 7 in 5 and 2, because I know that 8 + 2 will lead me to 10. This will eat up your time, but will little practice; you will save a lot of time later.
Practice few numbers
1) 14321 + 2341 + 1123
2) 2346 + 4634 + 7645
3) 6345 + 34 + 642
So now that you have learned the easier method, you won't feel shameful in front of your friends, when you were asked to add few numbers and you were busy finding the calculator.
Summary:
We never count higher than 10, if the addition goes above 10, then we reduce that number with 10 so whatever is the remainder we take it and than carry the count of total such reduces that we made, if you think about it, it is same as the conventional method, but what we are doing is reducing the time required to calculate numbers higher than 10.
Like suppose you want to add 19 + 18 + 17 + 16, in the conventional method we would do it like 9 + 8 + 7 + 6 = 20 then carry 2 over the left hand side digit. In our method we are doing same but we remember how many times we added up to or crossed 10, so in the above case it will be 2, same as 2 in 10's place of 20, give it some thought.
Until next time, adios.
Permalink / 0 comments /
Table of Contents
Quantitative Aptitude - Arithmetic & Algebra
- Number System - Basics 1, Basics 2, Problem Set 1
- Arithmetic - Addition, Subtraction, Division, Multiplication, Problem Set 1
- HCF & LCM - HCF, LCM, Problem Set 1
- Fractions
- Surds and Indices
- Algebra - Basics 1
- Algebraic formula and their applications
- Symbol Based Problems
- Percentages
- Simple & Compound Interest
- Simple Equations
- Linear Equations in two variables
- Quadratic Equations
- Inequations
- Averages
- Ratio, Proportion & Variation
- Mixtures & Alligations
- Profit & Loss
- Partnership
- Stocks & Shares
- Time, Speed & Distance
- Races
- Work
- Pipes & Cisterns
- The Roman System of Notation
- Calender
- Clocks
Verbal Ability & Verbal Reasoning
- Intro - Sentence, Subject & Predicate
- Parts of Speech and Articles - Basics, Noun, Pronoun, Adjective, Verb, Adverb, Conjunction, Preposition, Interjection.
- Clauses, Idoms and Phrasal Verbs - Phrases, Clauses, Idioms, Phrasal Verbs.
- Common Errors - Pronoun Antecedent Agreement, Verb Tense Match, Parallel Construction, Misplaced Modifier, Dangling Modifier, Subject Verb Agreement, Prepositional Usage, Correct Adjectival Usage, Correct Usage of Articles, Sentence Correction.
- Jumbled Paragraphs and Sentence Patterns
- Fill in the Blanks - Logical Fill In the Blanks, Paired Logical Fill in the Blanks, Missing Link in a Paragraph, Complete the theme, Word repeated Maximum Number of Times
- Critical Reasoning - Premise, Assumption, Conclusion, Inference, Structure
- Odd Man Out, Analogies and Multiple Usage
- Summary
- Venny Diagrams and Syllogisms - Venn Diagrams, Syllogisms
- Definition Based Questions - Argument, Assertion and Counter-argument, Conclusions and Implicit Statements, Fact, Inference, Judgement, Probably True/False, Definitely True/False, Strong Argument, Weak Argument
Aesthetic Math
Drills:
Quant Questions
01, 02, 03, 04, 05, 06, 07, 08, 09, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20,
21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40,
English - Sentence Correction
01, 02, 03, 04, 05, 06, 07, 08, 09, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20,
21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40
English - Critical Reasoning
01, 02, 03, 04, 05, 06, 07, 08, 09, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20,
21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40
English - Reading Comprehension
01, 02, 03, 04, 05, 06, 07, 08, 09, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20,
21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40
English - Word List
Other Articles
Indra Nooyi's Graduation Remarks
Yale - 2006 Class Day Address
Devil's Advocate: Karan Vs. Arjun
Best of Luck!!
Permalink / 0 comments /The toughest exam, CAT: Gets even tougher
All the IIMs imposed a 50% cut-off marks criterion at the graduation level.- IIMs want to make CAT a two-tier exam for cutting down on the number of aspirants who take the final test
- The 50% cut-off marks criterion will shed at least 20,000 candidates
- Less candidates means less revenue as IIMs lose Rs 2 crore a year due to the cutoff marks bar.
Further Reading:
CAT wants to shed weight
IIMs fix 50 % as eligibility for CAT
Now, prelims and a final for CAT?
Now, IIMs plan CAT prelims
Number System - Basics 2
Previously we saw classification of numbers, we can further classify natural numbers (from 1 to infinity) as Prime and Composite.
Factor: Let x and y be two integers, if x divides y completely, means the remainder is zero, then we can say that x is a factor of y. Example, 6 and 3, where 3 divides 6 completely, hence 3 is a factor of 6. What are the other factors of 6? Find out.
Multiple: In the above example, 6 is a multiple of 3 and 2 both, hence 3 and 2 are factors of 6 and 6 is a multiple of 3 and 2.
1) Prime Numbers:
If a number has only two factors, unity and itself, then the number is said to be prime. Numbers like 2, 3, 5, 7, etc. For example if we list down the factors of 28 we have 1, 2, 4, 7, 14 and 28. We have more than 2 factors, suppose we list down factors of 31 we only have 2 factors, 1 and 31, hence we can say that 31 is a prime number.
2) Composite Numbers:
In the above example we listed down the factors of 28, which has more than 2 factors, hence such number is known as composite number.
Note: 1 is neither prime nor composite.
Prime numbers from 1 to 200:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199.
It would be helpful to remember primes till 100, because all the composite numbers are composed of prime numbers, we will explore this in later section.
Q1) How to find out if the given number is a prime?
A) Divide the number with all the primes less than its square root. Example, take 29, nearest square is 36, hence the square root of 29 will lie in between of 5 and 6, if the number is divisible by any of the primes less than 6, then it is not a prime number.
Q2) Why does this work?
A) If we divide the number n with its factor x which is greater than its square root, then the result of n/x will be a smaller number than the square root of n, hence we can safely determine if number is prime or not with the above test. We can even say when we multiply with numbers greater than its square root we will get a bigger number then the number itself, hence we just need to check the divisibility with smaller numbers than the square root of the number.
We can use the formula 6n ± 1 to find out prime numbers greater than 3, where n > 0. Example, 6(1) + 1 = 7 and 6(1) - 1 = 5, both 7 and 5 are primes, where n = 1. But it doesn't always work, try few numbers.
3) Relatively Prime or Co-Prime Numbers:
If two or more numbers does not have common factors other than 1 than they are said to be relatively prime or co-primes. In other words the HCF (Highest common factor) of the numbers is 1. We will see HCF in later section. Example, 14 and 15, the Factors of 14 are 1, 2, 7, 14 and the factors of 15 are 1, 3, 5, and 15. There are no common factors other than 1 between 14 and 15, hence they are said to be relatively prime.
Actually, the concept of relatively prime is always used when we reduce the fraction to its smallest term. Example, when we reduce 12/15, we cancel out 3 and we get 4/5, which does not have any more common factors, hence 4 and 5 are relatively prime.
4) Perfect Numbers:
If the sum of the divisors(factors) of a number n is equal to 2n then the number is said to be a perfect number. Example 28, factors of 28 are 1, 2, 4, 7, 14, 28. When we add all the factors of 28 we get 2 x 28 i.e 56. You can exclude the number n in the sum, then you will get the number itself rather than 2n, give it some thought.
The sum of the reciprocals of the factors of a perfect number is always 2.
Example, 1/1 + 1/2 + 1/4 + 1/7 + 1/14 + 1/28 = 2.
5) Even and Odd Numbers:
Numbers can be classified in two groups namely Even or Odd. Any number which is divisible by 2 is an even number can be denoted by 2n, all the other numbers are odd, means which are not divisible by 2 and can be denoted by 2n + 1.
Properties:
Addition or subtraction:
odd ± odd = even.
even ± even = even.
even ± odd = odd.
Multiplication:
odd x odd = odd.
even x even = even.
odd x even = even.
The base determines if the final result is even or odd.
even number raised to even or odd will result in even.
odd number raised to even or odd will result in odd.
Summing it up :
- Sum of any number of even numbers is even, eg. 2 + 6 + 8 = 16.
- Sum of even number of odd numbers is even, eg. 1 + 3 + 5 + 7 = 16.
- Sum of odd number of odd numbers is odd, eg. 5 + 7 + 3 = 15.
- If the product of numbers is even, at least one of the numbers has to be even.
- If the product of the numbers is odd, all the numbers have to be odd.
Some more observations:
The product of any 3 consecutive numbers is always divisible by 24 if the first number is even. Why? Because the factors of 24 are 8 x 3, any 3 consecutive numbers multiplied will contain these factors if the first number of the three is even.
If the first number of the 3 numbers is odd then the number will always be divisible by 6 and not 24. Why? Because the result will always contain the factors 2 x 3.
*Note: 2 is the only prime which is even.
Prime numbers play an important role in Number Theory. Understanding of primes, even and odd numbers is essential from the point of view of the exam. We will look into prime, even and odd numbers in more details later when I take up problems.
*TIP: As I mentioned earlier there won't be any silly question in CAT, like, is the number prime or not, but there are questions asked in which the terms are often used. Hence, the concept should be understood in and out.
Permalink / 2 comments /
Number System - Basics 1
Tuesday, April 25, 2006
Prehistoric men didn't had any method to count quantities, as someone said "Necessity is Mother of invention", holds true for this, they slowly evolved a method with which one can distinguish between quantities, count them, but not limited only to these. The earliest number system known in use was somewhere around 30,000 BC, used by Stone age people as Tally marks.
![]() The system was limiting, large numbers cannot be represented, then evolved Roman Number system, which also had limiting factors, zero was known but didn't have any existence.
The system was limiting, large numbers cannot be represented, then evolved Roman Number system, which also had limiting factors, zero was known but didn't have any existence.
Finally the evolution of Number system which we are using today, the Numerals from 0 - 9 of base 10, evolved. Life became easy and peaceful. This evolution was not an easy one, each species of human being from every corner of the world has contributed in every stage, in every level, the Greeks, the Indians, the Egyptians and many others.
Classification of Numbers:
1) Natural Numbers: All the positive numbers from 1 to infinity. {1, 2, 3, ...}
2) Whole Numbers: All the natural numbers with an introduction of 0. {0, 1, 2, ...}
3) Integers: Numbers including whole numbers and negative numbers. {..., -2, -1, 0, 1, 2, ...}
4) Rational Numbers: A number which can be expressed as a fraction p/q where q <> 0 (not equal / non-zero) and the number is terminating or recurring(periodic). {5/2 = 2.5}
5) Irrational Numbers: A number which cannot be expressed as a fraction p/q where q<> 0, irrational numbers have decimal expansions which are not terminating nor periodic. 2^1/2 (root 2)
6) Real Numbers: All the above numbers collectively known as real numbers. These numbers can be plotted on a number line.
7) Imaginary Numbers: Some numbers cannot be expressed such as square root of a negative number -1^1/2. Imaginary number is denoted by i. In other words those are not real numbers. {i = -1^1/2}
8) Complex Numbers: A combination of real numbers and imaginary numbers is known as complex number. {5 + 2i}
*TIP: Don't expect a direct question like, "Is the following number a rational or irrational number". CAT doesn't ask such silly questions. But the understanding of the above is crucial, questions will contain terms like rational number, real number, integer, which you need to consider while marking your answers.
Dreamer
Sunday, April 23, 2006
Q) Why have you chosen to Blog?
A) You can find notes for MBA entrance, problems, tip and tricks; its an effort to help aspirants to crack the same. One is welcome to post comments or write an alternate solution to the problems posted. It will help in contemplating my own thoughts and desires. No better place than a Blog.
Q) What's the rationale behind choosing the name MBA Fever for your Blog?
A) Regarding the name, It captures the spirit of the Blog, anyone who is preparing for MBA can relate to the title. It takes guts to crack monster like CAT, which is getting tougher and tougher day-by-day, and one can easily relate to the fever I am talking about. Once I was scratching my head, and it just popped.
Q) Why MBA?
A) Why Not? I think an MBA is a general degree, it is an "Investment for lifetime", which one needs to pursue. I Belive its an extension to your current degree. To survive in this competitive world one must be on the edge, the peak, the pinnacle.
One doesn't want to feel detached, one likes to work with like minded people, to tune with oneself and with others, MBA acts as a passage, which one needs to walk on.Nobody wants to reinvent the wheel; we can learn from mistakes of others and move on. Apart from this, I think it suits my persona.
Q) Are you going to write on other subjects too?
A) Yes, I will take an opportunity to write about varied topics like Movies, Music, Commerce, Economics, Law, Politics, Software development, Games, Latest happenings, News, Views, Opinions, basically anything under the sun.
I would like to make this a fora, a channel, rather than one-person centric, I would like your participation, if you want to post any articles on this Blog, and if you think it will help others, you are most welcomed.
Q) Where can one start from?
A) A good place to jump start would be from the central page, i.e Table of Contents page. All the topics and articles can be found there.
Q) How can one reach you?
A) Best way to get in touch would be to email me at mbafever@gmail.com, generally I try to reply most of the emails, due to time constraints it might take few days to go through all the emails that I receive.
Q) Is there any online presence other than this website?
A) Yeah, one can communicate with fellow aspirants and readers of MBA Fever blog at Yahoo Groups & Orkut Community
Q) Any final words?
A) This is just the beginning of the Journey. It's never late to play the game, you loose some, and you win some. Checkmate.
The author sometimes likes to write as a third person, he can't recollect from when did he start doing so.
Permalink / 1 comments /