Arithmetic - Basics 1
Thursday, April 27, 2006
Q) Why do we need to look into Arithmetic?
A) Of course we don't need to look into addition, subtraction, multiplication and division, if you are good with it. But theres nothing wrong in learning few tricks, we don't need to learn Vedic Maths, just few tricks to calculate faster. After all, its all about speed and accuracy, honey.
Take off!
First of all, one needs to be quick in adding numbers; this can be easily achieved if you are quick with adding one digit numbers. Every one knows 4 + 3 = 7, but it has to be in your visual memory. Can u tell the answer without calculating in your mind? If yes, then skip this section.
Bug your friends, brothers, relatives and your mom to quiz you, to ask you to add numbers. Following is the cheat sheet. Fit this in your visual memory.
When adding two numbers, one trick is to split any one of the number such that the other number can be composed as 10 when added with one part and then add the remaining part.
Example, take 8 + 6, you can spit 6 in two part 2 and 4, now add 8 with 2 which gives 10 and then add 4 to it, i.e. 14.
The easiest method to add large numbers is to start with higher order digits.
Suppose you want to add 8,500 + 2,000 + 900 + 85 + 9
1) 8,000 + 2,000 = 10,000 --- thousands places
2) 500 + 900 = 1,400 --- hundreds places
3) 10,000 + 1400 = 11,400 --- add the above two
4) 11,400 + 80 = 11,480 --- add with 10's place
5) 5 + 9 = 14 --- add the unit places
6) 11,480 + 14 = 11,494. --- the final answer
It is lot easier when done mentally, this method is meant to be done mentally ;)
There are easier ways to add numbers other than which we learned in school. In the next 5 minutes you will learn one of such method.
I will start adding all the unit places first then tens then hundreds so on and so forth. In the conventional method we add all the numbers and write down the unit's place of the sum and carry over the rest. In this method we will add the digits, but "we never count higher than 10". That means, whenever the running total becomes greater than 10, we replace the 10 with zero and go ahead, we need to keep track how many times we reduced the sum with 10, means, we need to count how many times we reduced the sum with 10 and carry that number to the left.
Suppose you want to add 14686, 15463 and 65367
Sum of all units' digits is
6 + 3 = 9
9 + 7 (sum exceeds 10 (i.e 16) so subtract 10 (i.e 16 - 10 = 6), remainder 6)
Now write down 6 and carry over 1, because the sum exceeded 10 just once.
14686 + 15463 + 65367 = ----6
Now add the tens places, don't forget to include the carry forward
Sum of all tens digits is
8 + 6 (sum exceeds 10 (i.e 14) so subtract 10 (14-10), remainder 4)
4 + 6 (sum is equal to 10 so subtract 10)
0 + 1(carry) = 1
Now write down 1 and carry over 2, because the sum exceeded 10 only twice.
14686 + 15463 + 65367 = ---16
Now add the hundreds places, don't forget to include the carry forward. Sum of all hundreds place digits is
6 + 4 (sum is equal to 10 so subtract 10)
0 + 3 + 2(carry) = 5
Now carry over the 1 and write down 5
14686 + 15463 + 65367 = --516
Now add the thousands places, don't forget to include the carry forward
Sum of all thousands place digits is
4 + 5
9 + 5 (sum > 10 subtract 10, remainder 4)
4 + 1(carry) = 5
Now carry over the 1 and write down 5
14686 + 15463 + 65367 = -5516
Now add the ten thousand places, don't forget to include the carry forward. Sum of all ten thousands place digits is 1 + 1 + 6 + 1(carry) = 9
And your final answer
14686 + 15463 + 65367 = 95516
I hope you understood the concept; we just need not exceed the running total more than 10. All this happens quickly if your are good with numbers. This might be tedious at first, but after solving few numbers you will find it lot easier than the conventional method. If you are not feeling comfortable, might be memorizing addition of one digit numbers will help. Like 7 + 8 = 7 + (3 + 5) = 15. In this example I am splitting the number 8 in 3 and 5 to make the addition easier, I know that 7 + 3 will lead me to 10. You can also split the 7 in 5 and 2, because I know that 8 + 2 will lead me to 10. This will eat up your time, but will little practice; you will save a lot of time later.
Practice few numbers
1) 14321 + 2341 + 1123
2) 2346 + 4634 + 7645
3) 6345 + 34 + 642
So now that you have learned the easier method, you won't feel shameful in front of your friends, when you were asked to add few numbers and you were busy finding the calculator.
Summary:
We never count higher than 10, if the addition goes above 10, then we reduce that number with 10 so whatever is the remainder we take it and than carry the count of total such reduces that we made, if you think about it, it is same as the conventional method, but what we are doing is reducing the time required to calculate numbers higher than 10.
Like suppose you want to add 19 + 18 + 17 + 16, in the conventional method we would do it like 9 + 8 + 7 + 6 = 20 then carry 2 over the left hand side digit. In our method we are doing same but we remember how many times we added up to or crossed 10, so in the above case it will be 2, same as 2 in 10's place of 20, give it some thought.
Until next time, adios.




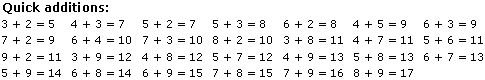
0 Comments:
Post a Comment